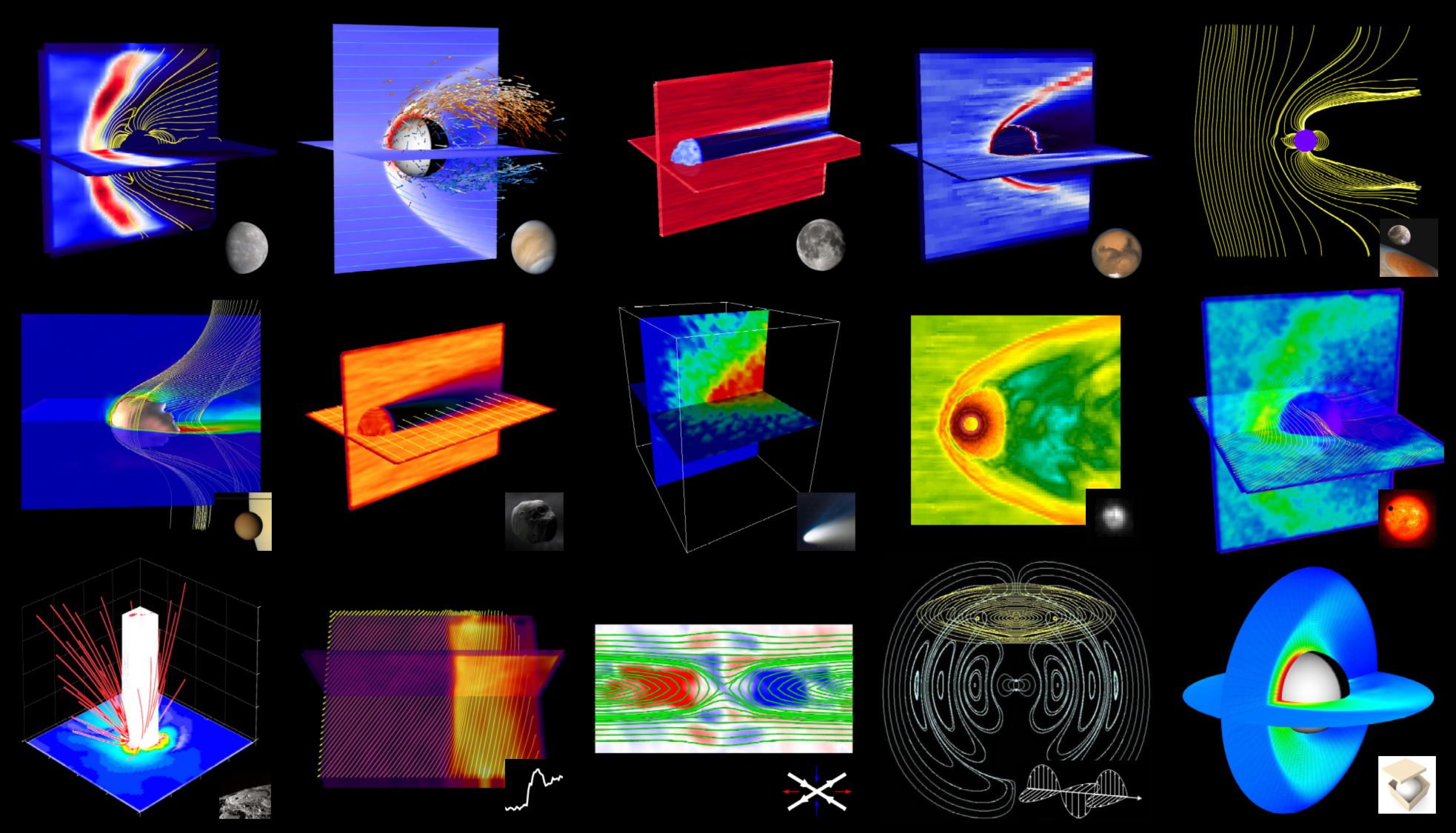
Hybrid codes are powerful tools to model space plasmas and plasma interactions of celestial bodies. In the hybrid approach ions are treated as particles while electrons form a fluid. The advantage of a hybrid model is that the ion velocity distributions need not be prescribed in advance as they evolve self-consistently in the model while leaving out electron kinetics, which are computationally expensive. Hybrid models are by definition of multifluid nature: they are able to solve plasma interactions of ion populations with different particle charges and masses. These model properties are very useful for studying flowing plasma interactions of planets, moons, comets and other objects since plasmas typically consist of several ion species and ion finite Larmor radius effects play an important role in many processes.
Equations of the hybrid model
The hybrid approach is based on the quasi-neutral hybrid (QNH) description of plasma. In the QNH model positively charged ions are treated explicitly as kinetic particles moving under the Lorentz force in electric and magnetic field. Electrons are modelled as a charge-neutralizing fuid. Ions are self-consistently coupled to the evolution of magnetic field by Faraday's law via ion charge density and ion current density, which are the source terms in the non-radiative Maxwell equations. Physical laws of the QNH model can be written as follows.
Ion dynamics are governed by the Lorentz force and Newton's second law (i = ion):
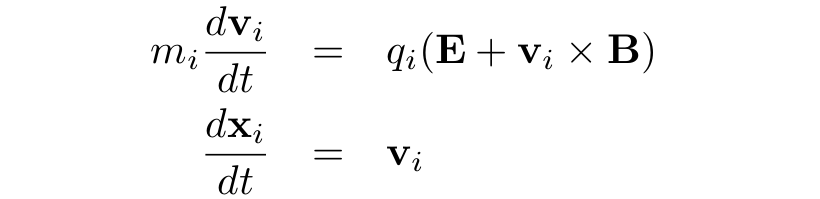
Electrons are considered implicitly as an inertialess fluid by the fluid momentum equation (Ohm's law):
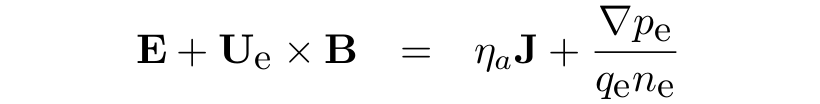
Ideal gas law and adiabatic assumption is used as the electron equation of state:
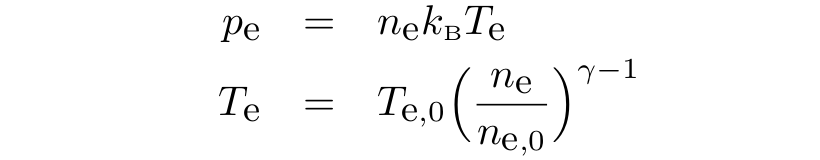
Quasi-neutrality condition of the plasma is (i = sum over all ions in a grid cell):
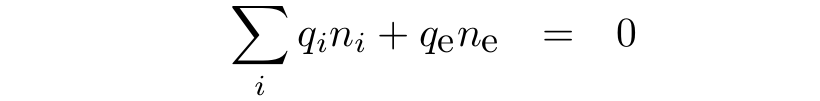
Electric current density is defined as:
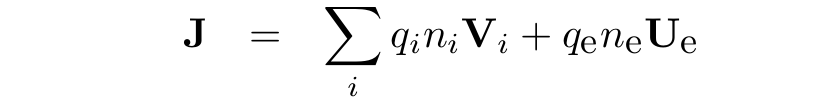
Electrodynamics follow from the non-radiative Maxwell equations:
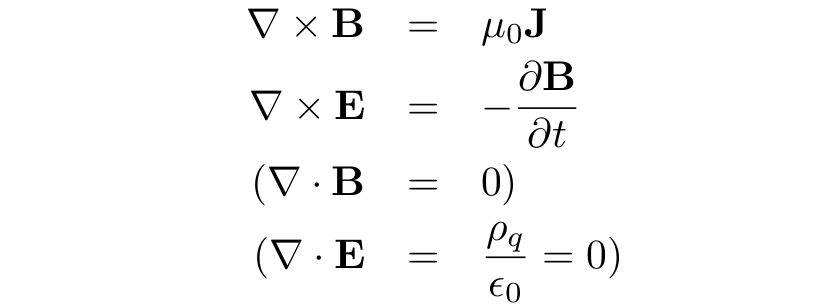
Symbols

Solving the model
The equations of the QNH model are solved by starting with known initial values for the ions (positions and velocities) and the magnetic field.
Time loop of the solver advances as follows:
Current density is obtained from the magnetic field via Ampère's law:

Electron charge density in a grid cell comes from the quasi-neutrality assumption:
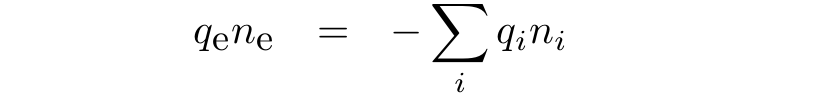
Electron velocity is determined from the definition of the total current density:
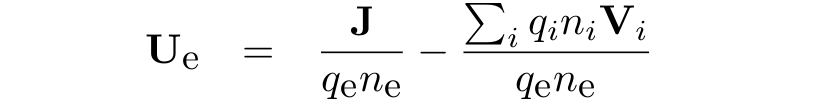
Electric field is calculated from the electron momentum equation and the ideal gas law as the electron equation of state:
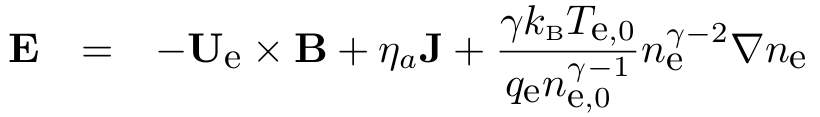
Magnetic field is advanced by Faraday's law:
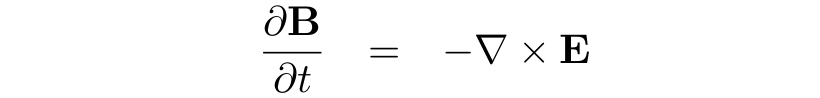
Ions are accelerated by the Lorentz force and moved by Newton's second law:
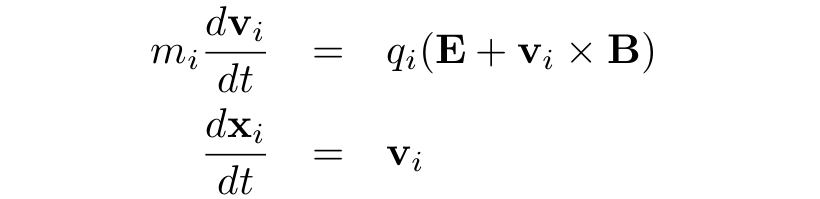
Numerical methods
The RHybrid and HYB codes use a Yee type staggered Cartesian grid (a spatial simulation mesh) to store the magnetic field on grid cell faces. The electric field is evaluated on grid cell nodes and grid cell edges, which guarantees that the divergence of the magnetic field remains stationary and zero.
Positively charged ions are modelled as macroscopic particle clouds (macroparticles or macroions) moving in the simulation domain (Particle-In-Cell, PIC, or Cloud-In-Cell, CIC, technique). Each macroparticle represents a number of real physical ions described by the statistical weight factor. Particles are accumulated in the mesh to determine the ion charge density and the ion current density (the ion moments). In the ion accumulation the weight factor and the cloud shape (e.g. trilinear) are used to evaluate how many physical particles in the cloud belong to each grid cell the cloud overlaps with.
In the HYB code both Cartesian or spherical coordinate systems can be used and the mesh is hierarchically refinable allowing increased spatial resolution where it is needed within the simulation domain. Further, HYB allows macroparticle splitting and joining to control the average number of computational ions in the domain. Ions can be joined (3->2) if too many macroparticles are found in a grid cell. And ions can be splitted (1->2) if too few macroparticles are found in a grid cell. The conservations laws are satisfied in the particle splitting and joining. This technique is needed when using several leves of grid refinements to allow enough (but not too many) macroparticles to be modelled in the simulation.